Appartient au dossier : Le nombre d’or : mathématiques et beauté
Le Nombre d’or d’hier à aujourd’hui
Ce nombre fascine depuis très longtemps. On le rencontre partout dans l’art, la philosophie, l’économie, la géographie et dans les mathématiques. On ne peut en parler sans évoquer les grandes figures, mathématiciens, philosophes, artistes, etc., qui d’une façon ou d’une autre ont fait avancer la connaissance du nombre d’or.
Dès l’Antiquité

Les origines du nombre d’or semblent remonter aux Pythagoriciens ; dès le VIe siècle avant Jésus Christ, cette confrérie, milieu d’une intense culture mathématique, a attiré les esprits curieux de sciences et les mystiques. Le pentagramme, étoile à cinq branches, symbole comportant le nombre d’or et ayant une valeur symbolique pour les Grecs, aurait été le signe de ralliement des pythagoriciens.
Hérodote (Ve siècle avant J.-C.)
Les textes du tout premier historien, Hérodote, au Ve siècle avant J.-C. conduisent à penser que les Égyptiens utilisèrent le nombre d’or pour bâtir la grande pyramide de Khéops et que les grecs, qui l’appelaient section dorée, lui ont subordonné la conception du Parthénon .
Phidias (490-430 av. J.-C.)
Sculpteur et mathématicien grec, il étudia, dit-on, la section dorée et l’appliqua aux ornements qu’il réalisa pour le Parthénon. Son œuvre la plus célèbre, la statue de Zeus à Olympie, faisait partie des Sept merveilles du monde antique. Il serait l’un des premiers à avoir intentionnellement utilisé la divine proportion. Aucune de ses œuvres originales n’a survécu, mais l’histoire en a conservé plusieurs copies romaines. De nombreux auteurs de l’Antiquité se feront l’écho de la grande influence qu’il exerça sur la sculpture de son époque.
Platon (427-347 av. J.-C.)
Dans ses travaux sur les sciences naturelles et la cosmologie, il évoque l’existence d’une certaine proportion, considérée comme la plus opératoire de toutes les corrélations mathématiques et la clé de la physique cosmique.

Euclide (325-265 av. J.-C.)
Sa première trace écrite remonterait à l’an 300 av. J.-C. dans Les Éléments de géométrie, œuvre maitresse d’Euclide (325-265 av. J.-C.) qui eut une influence considérable dans le développement des mathématiques universelles et compte parmi les ouvrages fondamentaux de notre culture. On y trouve la somme des connaissances mathématiques de l’époque. Euclide souhaitait composer une sorte d’encyclopédie qui puisse servir de manuel d’enseignement des mathématiques. Egalement, il voulait démontrer des résultats et construire une théorie mathématique. Dans Les Éléments, il énonça un théorème qui traduisit pour la première fois le nombre d’or en langage mathématique.
Euclide dirigeait en l’an 300 le département de mathématiques au Musée (temple des Muses) de la ville d’Alexandrie. Ce lieu était le principal centre scientifique de toute la Méditerranée de l’époque. C’est ici qu’Euclide vécut. Il était considéré comme l’un des grands talents de son époque. Son influence perdura à travers l’histoire si bien que dans les années 1930, le mot d’ordre d’un groupe de mathématiciens sous le nom de Nicolas Bourbaki qui voulait moderniser les mathématiques fut : « A bas Euclide ! »
Au Moyen âge

Leonardo Pisano (1170-1250)
C’est durant cette époque que vécut Leonardo Pisano, plus connu sous le nom de Fibonacci. Il introduisit la suite qui porte son nom dans le traité Liber Abaci, (livre de l’Abaque). Le Liber Abaci, en plus de démontrer les avantages des chiffres arabes, aborde la théorie des nombres, contient des problèmes d’algèbre du premier degré et parle de comptabilité marchande. Leonardo Pisano découvrit les propriétés surprenantes d’une suite numérique (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…). Chaque terme s’obtient par la somme des deux précédents : ainsi, lorsqu’on divise chaque nombre par le nombre précédent, on obtient des valeurs plus ou moins égales à Phi. Exemples : 89 : 55 = 1,618037… Ainsi, l’algorithme de récurrence de Fibonacci est si puissant que, quelques soient les nombres de départ, la suite des rapports de ces termes converge toujours vers Phi ou nombre d’or.
Léonardo Pisano, dont le père était un marchand italien, s’initia aux mathématiques à partir de la comptabilité. Ses voyages marchands en Afrique du nord lui donnèrent l’occasion de s’initier aux mathématiques arabes. Il apprit le système de numérotation arabo-indou et en comprit les avantages par rapport aux méthodes en vigueur dans l’Italie de l’époque ou les abacistes employaient l’abaque et la numérotation romaine. En Europe, il en devint le défenseur et c’est à lui que nous devons l’apparition des chiffres arabes dans notre culture.
À la Renaissance
Les intellectuels de la Renaissance s’intéressaient aux mathématiques, à la géométrie et aux lois de la proportion.
Leon Luca Pacioli (1445-1517)
Luca Pacioli fut avec Léonard de Vinci à l’origine de l’introduction du nombre dans le monde de la beauté et de l’art. Moine bolognais et professeur de mathématiques, il compose en 1498 un traité, De divina proportione (La Divine Proportion), illustré par Léonard de Vinci avec son étude du corps humain selon Vitruve. Il introduit le terme de divine proportion. Il considère que le nombre d’or a des propriétés esthétiques et qu’on le retrouve dans l’architecture et la peinture.
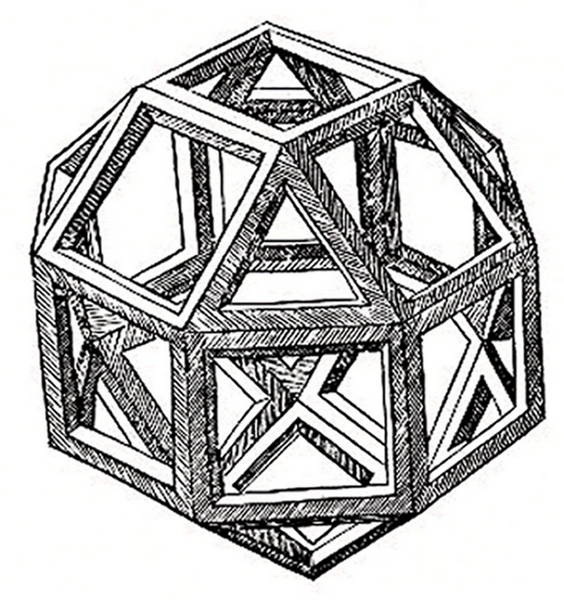
De divina proportione fixe les proportions à respecter pour atteindre la beauté suprême, sous forme d’une réflexion sur la géométrie. Dans cette œuvre apparaissent les fameux soixante polyèdres dessinés de la main de Léonard de Vinci et son non moins célèbre homme de Vitruve, basé sur Phi, revisité à maintes reprises au fil des années. Ce livre rassemble les éléments indispensables des œuvres de la culture occidentale : une époque, la Renaissance ; un lieu, l’Italie ; et les protagonistes fondamentaux, les artistes, architectes, mathématiciens et philosophes ayant marqué l’histoire et l’art européens.
Trois artistes importants ont exercé une influence sur Pacioli : Léon Batista Alberti (1404-1472), Piero della Francesca (1422-1492) et Léonard de Vinci (1452-1519). Ils avaient tous étudié les mathématiques, les sciences, l’ingénierie et ,
l’architecture.

Dans le portrait de Luca Pacioli datant de 1495, peint par Jacques de Barbaru et exposé au musée de Capodimonte de Naples, le mathématicien apparaît en habit franciscain, enseignant la géométrie euclidienne à un jeune noble (le duc d’Urbino). Maître et élève sont entourés de polyèdres et d’outils géométriques. À gauche pend un polyèdre appartenant à la famille des solides d’Archimède. Beaucoup de ces polyèdres apparaissent dessinés par Léonard de Vinci dans De divina proportione.
Leon Battista Alberti (1404-1472)
Avec le Traité de la peinture de Léon Battista Alberti, apparaît l’oeuvre fondatrice de la perspective. Dans cet ouvrage sont apparues des idées qui ont imposé de nouvelles règles comme celle qu’exprime cette phrase : « Le premier prérequis pour un peintre est de connaître la géométrie ». Par ces nouvelles règles, Alberti souhaitait guider le travail des artistes. Dans De statuta, il expose les proportions du corps humain ; dans De pictura, il conçoit la première définition de la perspective scientifique ; dans De reaedificatoria, il décrit sa conception de l’architecture moderne, complètement imprégnée de la proportion d’or.
Alberti reste une figure emblématique de la Renaissance. Il étudia principalement l’architecture, les mathématiques et la poésie mais aussi la linguistique, la philosophie et la musique. Il travailla comme architecte pour le célèbre commerçant et humaniste Giovanni di Paolo Rucellai, pour qui il réalisa la façade de la Santa Novella, basée sur la proportion d’or. Il réalisa aussi des oeuvres majeures de l’histoire de l’architecture comme la Villa médicis, le Palais Rucellai.
Léonard de Vinci (1452-1519)
Léonard de Vinci continua l’étude la perspective. Il fut l’homme de la Renaissance par excellence. Ses contributions englobent des domaines très différents les uns des autres tels que, la peinture, l’architecture, les mathématiques, la physique chimie, le génie civil, la technologie, etc. Il excellait dans tout ce qu’il faisait et ses travaux se sont révèlés importants dans leurs domaines respectifs. Il fut aussi le théoricien de l’art et de la peinture. Il défendit ardemment leur association avec les mathématiques :
« Que nul ne lise mes œuvres s’il n’est mathématicien. »
Il intervient comme illustrateur dans De divina proportione, écrit par Luca Pacioli. Celui-ci souligne l’importance des études mathématiques de de Vinci dans le domaine artistique. Ses dessins ainsi que L’Homme de Vitruve, sont devenus de véritables témoignages d’un courant de pensée qui réunissait sensibilité artistique et scientifique, l’idéal humaniste.
Albrecht Dürer (1471-1528)
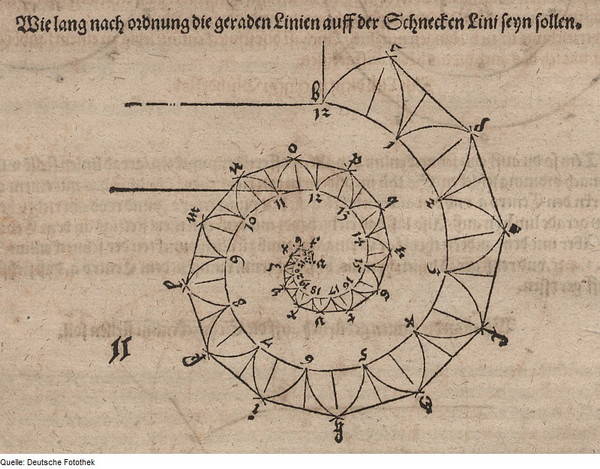
Le plus remarquable sucesseur de Léonard de Vinci fut Albrecht Dürer. Grande figure de la Renaissance, il découvrit l’œuvre mathématique de Pacioli lors d’une visite à Venise. Il publia en 1525 Instructions pour la mesure à la règle et au compas de figures planes et solides, plus connu sous le nom de La Mesure. En plus d’y exposer sa philosophie de la beauté qui réside dans l’harmonie des proportions, cet ouvrage décrit la construction d’un grand nombre de courbes comme la spirale basée sur le nombre d’or, connue depuis comme la spirale de Dürer.
Dans l’ensemble son œuvre peut être considérée comme le début de la géométrie descriptive.
Aux XVI –XVIIe siècle
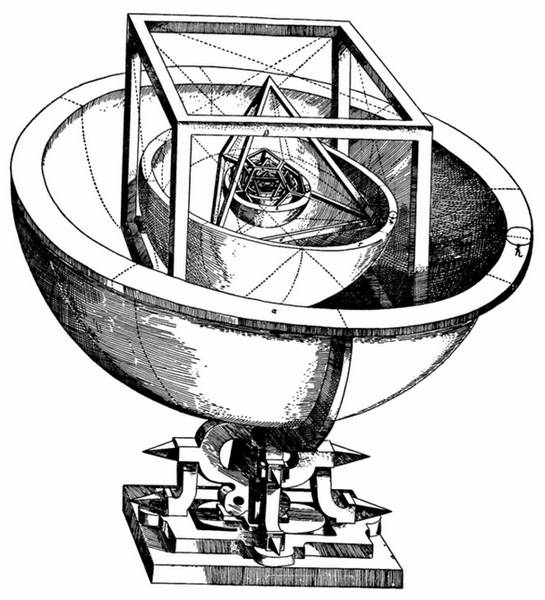
Johannes Kepler (1571-1630)
Astronome et mathématicien, il découvrit le caractère elliptique du mouvement des planètes autour du soleil et dévoila également la correspondance évidente entre la divine proportion et la suite de Fibonacci, où chaque nombre s’obtient par la somme des deux précédents. Il est fasciné par le nombre d’or dont il dit :
« La géométrie contient deux grands trésors : l’un est le théorème de Pythagore, l’autre est la division d’une ligne en moyenne et extrême raison ; le premier peut être comparé à une règle d’or, le second à un joyau précieux. »
Au XIXe siècle
L’intérêt pour le nombre d’or ressurgit au milieu de ce siècle. Les termes de section dorée puis nombre d’or apparaissent. C’est avec les travaux du philosophe allemand Adolf Zeising (1810-1876) que le nombre d’or devient un véritable système pour la compréhension de nombreux domaines, tant artistiques comme l’architecture, la peinture, la musique, que scientifique avec la biologie et l’anatomie. Une dizaine d’année plus tard il publie un article sur le pentagramme « manifestation la plus évidente et la plus exemplaire de cette proportion ». Une lecture de la métaphysique pythagoricienne lui permet de conclure à l’existence d’une loi universelle fondée sur le pentagramme et donc, sur le nombre d’or.
En France, l’idée de codifier de manière scientifique la beauté séduit. On mesure le Louvre, l’Arc de triomphe, les cathédrales avec attention. Des délégations partent mesurer la taille des pyramides, des monuments antiques tels le Parthénon ; Charles Henry (1859-1926), un érudit proche des positivistes, associe au nombre d’or une théorie de la couleur des lignes. Il aura une influence non négligeable sur des peintres tels Seurat, Signac ou Pissarro.
Au XXe siècle
Durant toute la première moitié du siècle, et malgré le déclin du positivisme, la popularité du nombre d’or ne faiblit pas. Les théoriciens du XXe siècle considèrent qu’il est la loi fondamentale qui imprègne la nature et les arts ; Ils rejoignent ainsi les courants scientistes et théosophiques du Symbolisme de la seconde moitié du siècle qui influenceront souvent les artistes.
Matila Ghyka (1881-1965)
Prince roumain écrivain et mathématicien, il fut l’un des spécialistes de la proportion d’or. Il publia plusieurs ouvrages désormais classiques comme Esthétique des proportions dans la nature et dans les arts (1927) et Le Nombre d’or (1931), préfacé par Paul Valery, qui remit à l’ordre du jour ce principe dans la culture européenne. Dans ces ouvrages, il présenta la thèse suivante : les artistes grecs de l’antiquité classique utilisaient sciemment la proportion d’or. Cette hypothèse est pourtant toujours sujette à débat et n’est pas unanimement admise.
L’Esthétique des proportions dans la nature et dans les arts est une synthèse des travaux de Ghyka sur la symbolique des formes, la section dorée, les partitions de l’espace, les entités géométriques, les lois de croissance harmonieuses, les canons créateurs d’une beauté qui est aussi esprit. La tradition pythagoricienne, qui plonge ses racines dans les anciennes civilisations proche-orientales, a transmis une philosophie de la forme pure, reposant sur des idées-nombres, qui est le secret de toute architecture vivante. La connaissance de cette géométrie, à la fois technique et symbolique, ainsi que la méditation approfondie de la science de l’espace, sont indispensables « à ceux dont le pinceau, le ciseau ou le cordeau doivent fixer ou créer des formes », reprenant la vision des Bramante, Raphaël ou Michel-Ange.
Publié le 20/11/2014 - CC BY-NC-SA 4.0
Sélection de références
Le Nombre d'or. Le langage mathématique de la beauté
Fernando Corbalan
RBA France, 2013
À la Bpi, niveau 2, 51(02) MON 1
Les Nombres. Secrets d'hier et d'aujourd'hui
Philippe Boulanger (dir.)
POLE, 2008
À la Bpi, niveau 2, 511.9 NOM
L'Univers des nombres. De l'Antiquité à Internet
Hervé Lehning
Ixelles éditions, 2013
Depuis les abaques jusqu’aux ordinateurs, la saga des nombres racontée à tous, par Hervé Lehning, enseignant en écoles d’ingénieurs, puis professeur de mathématiques spéciales au Lycée Janson-de-Sailly à Paris, rédacteur en chef du magazine Tangente.
Les champs signalés avec une étoile (*) sont obligatoires