Appartient au dossier : Le nombre d’or : mathématiques et beauté
Le Nombre d’or, mythe ou réalité ?
L’expression « nombre d’or » évoque la loi unique d’une harmonie universelle et le symbole même du beau. Il symboliserait la perfection, donnerait une explication universelle du sentiment esthétique, résumerait la géométrie de la beauté. Mais s’agit-il d’un mythe ou d’une réalité ?
Où trouve-t-on le nombre d’or ?
A vrai dire on le voit partout, dans la philosophie, la spiritualité, l’art, l’économie, dans la nature et dans les mathématiques. Beaucoup considèrent qu’on exagère son importance dans le domaine de l’esthétique et que le rôle mystique qu’on lui attribue est une imposture. Ils préfèrent se limiter à son aspect purement mathématique. Le nombre d’or est un concept simple qui se retrouve partout autour de nous. Le monde qui nous entoure est peuplé de rectangles dont beaucoup sont dorés : le rapport entre la longueur et la largeur est égal à Phi soit 1,618… Ces rectangles se retrouvent dans la nature (voir « Nature et symétrie « ) mais beaucoup sont construits par l’homme.
Ainsi les artistes croient à l’existence d’une proportion privilégiée permettant d’obtenir harmonie et beauté. Une belle peinture, une statue, un monument, la musique… sont équilibrés et organisés avec élégance autour de la proportion. Le nombre d’or est très souvent la clé de l’équilibre d’un tableau ou d’une construction.
Il est certain que l’harmonie propre au nombre d’or s’est glissée dans la construction des cathédrales gothiques comme dans l’architecture contemporaine grâce à le Corbusier. Il a également inspiré les tableaux de Léonard de Vinci, Degas, Georges Seurat et plus près de nous de Mondrian.
Au delà des facilités techniques proposées par tous ces encadrements géométriques, on ne peut négliger l’hypothèse d’une aspiration, même inconsciente, à connaître, enfin, la loi unique de l’harmonie universelle.
Le nombre d’or en peinture
La proportion d’or est visible dans ces trois exemples de peintures. Souvent elle naît d’une volonté consciente de l’artiste ou d’une simple intuition. Elle est parfois clairement visible, parfois seulement perçue, ressentie.

La Dernière Cène
Les éléments de la composition de ce tableau de Léonard de Vinci (1452-1519) ont des proportions d’or et dissimule diverses formes du nombre d’or, en particulier le rectangle. Dans cette oeuvre, le rectangle d’or définit aussi bien les dimensions de la table que la disposition des disciples autour du Christ. Il en est de même pour les murs de la pièce, ainsi que les fenêtres du fond. De façon générale, les peintres de la Renaissance influencés, consciemment ou non par la proportion utilisèrent le rectangle d’or, les spirales d’or, les triangles et les pentagrammes à tous les niveaux de détails.

Le Champ de course de Degas
Des divisions simples aident Degas à disposer les personnages et objets à la surface de la toile.
Pour la composition de ce tableau, Edgar Degas (1834-1917) a, par exemple, utilisé le rectangle d’or.
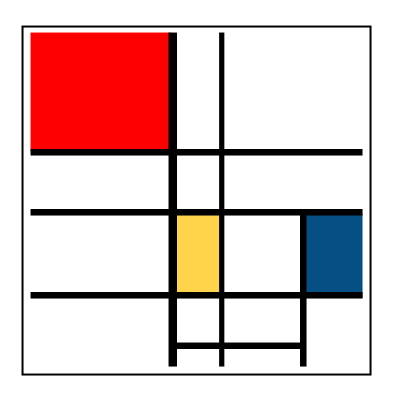
Les tableaux de Mondian
Rompant avec la figuration, Mondrian (1872-1944) découvre ou invente l’abstraction géométrique. Son langage pictural est basé sur les couleurs primaires (rouge, bleu, jaune), sur les non-couleurs (blanc, gris, noir) et sur des éléments géométriques prédéfinis. Pour composer sa toile, il combine ces éléments en obéissant au principe de la divine harmonie. Il se donne comme unique objectif l’harmonie des rapports : rapport des positions, rapport des proportions, rapports des couleurs. Il en résulte une présence très forte du nombre d’or dans l’oeuvre de Mondrian. Les formes géométriques cernées de gris ou de noir occupent toutes ses toiles.
Le nombre d’or en architecture
A toutes les époques, les architectes ont utilisé la proportion d’or. Certaines constructions depuis l’Egypte ancienne, telle la grande Pyramide de Keops, reposent sur le nombre d’or. Les arcs de triomphe de Rome également. Le Parthénon est, de toutes les constructions de l’Antiquité l’exemple le plus représentatif de l’usage classique de la proportion d’or.

Les églises et les cathédrales obéissent aux lois de la proportion divine. Les bâtisseurs du Moyen-âge ont élaboré ces constructions en les basant sciemment sur des nombres irrationnels tels le nombre d’or. Ils avaient la conviction qu’en créant la Terre et l’Univers, Dieu leur avait laissé tous les principes qu’il avait mis en oeuvre. Les retrouver, c’était le rejoindre.

Plus près de nous Le Corbusier (1887-1965) apporta sa contribution à l’histoire du nombre d’or. Il inventa sa propre échelle, basée sur les proportions d’or mais adapté à l’époque moderne. En réponse à L’Homme de Vitruve, il imagina L’homme de Modulor.
Parmi les nombreuses réalisations qu’il conçut, l’immeuble de l’ONU qui intègre trois rectangles d’or visibles sur la photographie ci-contre.

Pour calculer la structure de la Cité du numérique du Futuroscope de Poitiers, l’architecte Denis Laming s’est appuyé sur le nombre d’or. Le prisme de verre triangulaire sur lequel est basé une sphère blanche en polyester, est calculé selon les proportions du nombre d’or.

via Wikimedia Commons, 2006
De nombreux artistes contemporains se sont inspirés du nombre d’or, l’ont intégré dans leurs œuvres.
Ainsi, la suite de Fibonacci devient un élément artistique pour ces réalisations de Mario Mertz (1925-2003), artiste contemporain italien, représentant du courant de l’Arte Povera. Il introduit dans ses œuvres la suite de Fibonacci comme « symbole de l’énergie inhérente de la matière et de la croissance organique », en plaçant les chiffres réalisés au néon soit sur ses œuvres soit dans des lieux d’exposition.
Du mythe à la réalité Dans tous les cas, le nombre d’or est un sujet hautement sensible, voire passionnel, qui peut susciter le septicisme, comme l’adhésion, er même la croyance.
Consciemment ou non, les partisans du nombre d’or ne se sont-ils pas inspirés des ouvrages du mathématicien et philosophe de l’art roumain Matila Ghyka : L’esthétique des proportions dans la nature et dans les arts (1927) et Le nombre d’or (1931) ?
En effet cet auteur semble être à l’origine de ce mouvement qui établit la prééminence du nombre d’or et du mythe qui s’y rattache. Les sources de Ghyka sont pour l’essentiel germaniques. C’est bien en Allemagne, au milieu du XIXè siècle, que se situe la naissance du mythe où les études du philosophe Adolf Zeising et du physicien Gustav Theodor Fechner se sont imposées. Il les régénère, en explore la mathématique pour établir le très célèbre nombre d’or. Pour Ghyka, les artistes grecs de l’antiquité utilisaient délibérément le Nombre d’or. De nombreux auteurs, dans son sillage, ont été séduits par cette thèse qui s’appuie sur les Pythagoriciens, et ont eu recours à la section d’or pour réaliser leurs oeuvres.

Pourtant, selon Marguerite Neveux, qui a été maître de conférences en histoire de l’art à l’université Paris-I, ce mythe ne résiste pas à un examen attentif : par exemple, Ghyka se fonderait sur des mesures approximatives: pour trouver le nombre d’or dans la façade du Parthénon, il est obligé de prendre quelques marches de plus de la façade elle-même. Cette historienne d’art, procède dans sa Radiographie d’un mythe (1995 et réédité en 2014 ) à la réévaluation critique du rôle du nombre d’or. Cette édition comprend un chapitre inédit sur les avatars culturels récents de La divine proportion tel le livre écrit par Dan Brown en 2003, Da Vinci code.
Elle s’interroge sur les raisons de son succès et pour cela déconstruit le nombre d’or en présentant « les enjeux théoriques, les axiomes de départ, les légitimités invoquées c’est-à-dire comment s’est opèré le mécanisme de mystification », car le nombre d’or est un sujet particulèrement délicat.
Elle pose un certain nombre de questions : « Le nombre d’or détiendrait-il aussi de réels pouvoirs esthétiques, sans faire appel au mystique, ni aux mythique ?
Cette question en appelle une autre : Pourquoi ce nombre a-t-il pu à ce point séduire, ou plus simplement susciter l’intérêt de philosophes, de médecins, d’esthéticiens, de religieux, d’artistes ? […]
Quel besoin profond satisfait-il ? Ce besoin est-il nouveau ? »
Marguerite Neveux tente d’y répondre, sans ignorer ce que le sujet cache et comporte de plans, d’angles et de points de vue.
Son ambition est de contribuer à clarifier un symbole d’autant plus vivace qu’il nourissait et se nourrit encore d’une autorité certaine.
Publié le 20/11/2014
Sélection de références
Architecture et géométrie sacrées dans le monde : "à la lumière du nombre d'or"
Ribordy, Léonard (1939-....)
Éd. Trajectoire, 2010
A la Bpi, niveau2, 722 RIB
Le nombre d'or : clé du monde vivant
Rougié, Maurice (1884-1953)
Dervy, 2001
A la Bpi, niveau 2, 190 MAT
Maths & arts plastiques
Bibliothèque Tangente, H.S. 23
POLE, 2005
A la Bpi, niveau 2, 519.8 MAT