Appartient au dossier : Le nombre d’or : mathématiques et beauté
Nombre d’or et géométrie
Le nombre d’or est un nombre irrationnel découvert par les Grecs classiques. Sa première trace écrite remonte à l’an 300 avant Jésus-Christ dans les éléments de géométrie d’Euclide qui le définit ainsi : « partage d’une droite en moyenne et extrême raison ».
Le symbole Φ (lettre grecque Phi) ne lui a été attribué qu’au début du 20e siècle. Il est communément appelé nombre d’or ou divine proportion.
En ce qui concerne sa formule mathématique, elle peut s’écrire de plusieurs manières .Sa valeur est de 1+√5 sur 2, soit approximativement 1,61803398875 ou sous son aspect algébrique, l’équation x2 = x+1.
C’est par la géométrie que nous pouvons approcher le nombre d’or.
Le rectangle d’or
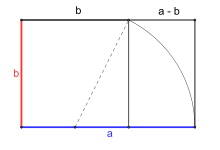

Un rectangle est dit d’or quand la proportion des deux côtés est égale au nombre d’or. Les résultats du quotient entre les longueurs du grand côté et du petit est égal à Phi, soit 1,618…
Pour se faire une idée de ce qu’est un rectangle d’or, il suffit de regarder les nombreux objets de notre quotidien telle une carte de paiement : le résultat du quotient entre les longueurs du grand côté et du petit est très proche de Phi.
La spirale d’or
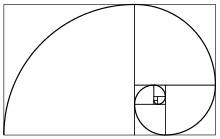

« NautilusCutawayLogarithmicSpiral ». [CC-BY-SA 3.0] via Wikimedia Commons
Le langage mathématique a étudié et décrit de nombreuses variétés de spirales. Elles ont toutes en commun leur mouvement circulaire autour d’un point fixe, dont elles s’écartent progressivement.
La spirale d’or, celle qui a pour base le nombre d’or, est dite spirale logarithmique. Sa croissance a la perfection de toutes les autres manifestations du nombre d’or. Elle contient en elle l’ensemble des propriétés qui fondent l’équilibre et l’harmonie de Phi. On retrouve ces spirales dans la nature, l’agencement des pétales d’une rose, la forme d’un coquillage (même si toutes ne sont pas reliées au nombre d’or).
Le pentagramme
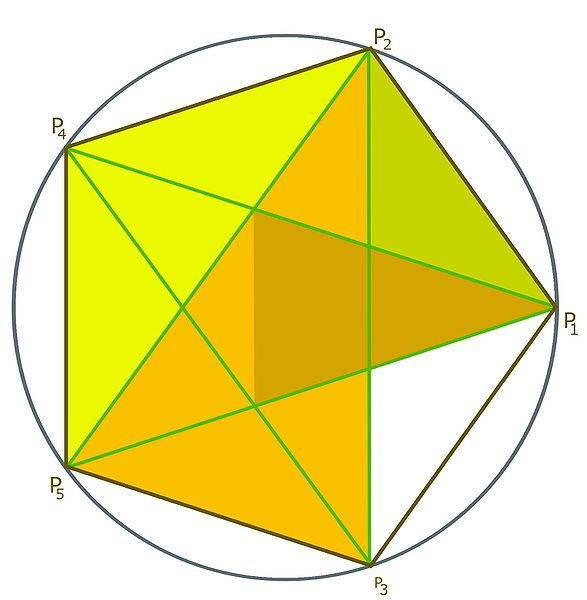

Le pentagramme, c’est-à-dire la figure composée de cinq diagonales du pentagone (cf figure à droite), contient aussi de multiples proportions de moyenne et d’extrême raison. Elles s’expriment simplement à l’aide de triangles isocèles dont les longueurs des côtés sont en proportion d’or.
Cette étoile à cinq branches est liée également au nombre d’or. On pense que c’était le signe de ralliement des Pythagoriciens pour qui le chiffre 5 était le signe de l’harmonie. Il était considéré par les anciens comme un symbole de perfection et de beauté. On le retrouve dans des créations artistiques, notamment dans les rosaces des cathédrales.
Le polyèdre

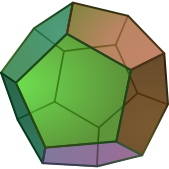
Le polyèdre est une figure solide à trois dimensions, dont les faces sont des polygones qui se rencontrent selon des segments de droites appelés arêtes.
Cinq polyèdres peuvent s’inscrire dans une sphère, symbole de l’Univers donc de l’absolu : le tétraèdre (quatre faces), l’hexaèdre ou cube (six faces), l’octaèdre (huit faces), le dodécaèdre (douze faces) et l’icosaèdre (vingt faces). Tous n’ont pas la même relation avec Phi. Ceux qui ont la relation la plus proche avec le nombre d’or sont le dodécaèdre et l’icosaèdre. Le nombre Phi se manifeste dans les expressions qui nous donnent le volume et la superficie (la somme des aires des faces) des deux polyèdres. Dans les pyramides, la présence du polyèdre témoigne de la perception de cette notion depuis les temps anciens.
La Suite de Fibonacci
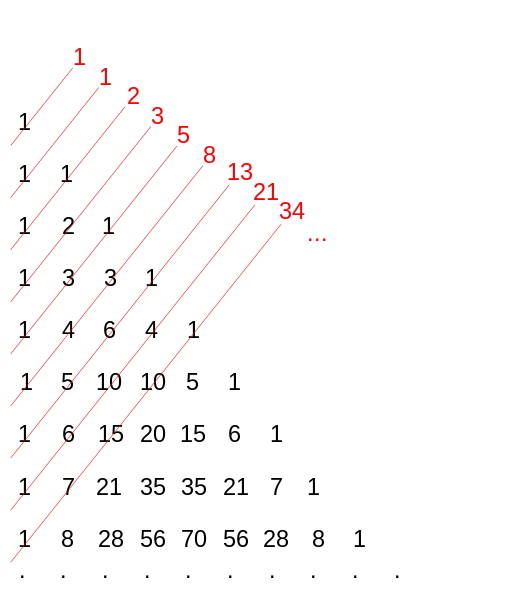

Au moyen âge, le mathématicien Léonardo Pisano est l’auteur d’une suite de nombres : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, etc., dans laquelle chacun d’eux est la somme des deux précédents. On constate que cette suite converge vers le nombre d’or : plus cette suite s’allonge, plus le rapport de deux nombres successifs se rapproche de phi. Les relations entre la proportion d’or et la suite de Fibonacci sont multiples.
Cette suite a de remarquables propriétés que l’on retrouve dans de nombreuses plantes, entre autres dans la fleur de tournesol ou dans le chou romanesco. La majorité des plantes a un nombre de pétales de 3, 5, 8, 13, 21, 34, 55 ou 89. Les pétales ne sont pas les seuls à faire intervenir la suite de Fibonacci.
Dans le chou romanesco l’aspect fractal est quasiment parfait. Les spirales que l’on observe ont une forme très régulière, partant du centre et s’agrandissant quand on s’éloigne vers la périphérie. Le nombre de ces spirales est toujours un nombre de la suite de Fibonacci.
Publié le 20/11/2014 - CC BY-NC-SA 4.0
Sélection de références
La divine proportion par la géométrie et les nombres
Ribordy, Léonard
Trajectoire, 2012
A la Bpi, niveau 2, 511.9 RIB
Le beau livre des maths : de Pythagore à la 57e dimension
Pickover, Clifford A.
Dunod, 2010
A la Bpi, niveau 2, 51 PIC
Le mystère des nombres : odyssée mathématique à travers notre quotidien
Du Sautoy, Marcus
Ed. Héloïse d'Ormesson, 2014
A la Bpi, niveau 2, 511.9 SAV
djelloul sebaa : 7/03/2021 23:47
Bonjour.
Soit l’équation x^2 – x -1 =0 qui admet comme l’unique solution positive x1 =( 1 + (5)^1/2)/2
Soit l’équation x^2 -x -d = 0 qui ……………………………………………………….x1 =(( 1 + (1 + 4.d )^1/2)/2.
le nombre ( 1 + (5)^1/2)/2 s’appelle le nombre d’or
le nombre (( 1 + (1 + 4.d )^1/2)/2 s’appelle le nombre d’or generalisé avec d réèl positif différent de 1.
Cordialement.
Djelloul Sebaa
Fabienne Charraire, Webéditrice, Balises : 25/03/2021 10:56
Si vous vous intéressez aux définitions mathématiques du nombre d’or, le site pédagogique Images des mathématiques en propose plusieurs mais toutes équivalentes au sens où elles définissent le même nombre.
Les champs signalés avec une étoile (*) sont obligatoires